CELL DYNAMICS
A priority to understanding of leukocyte dynamics lies in obtaining information on its rheological and mechanical properties. Mechanics of leukocyte has been studied considering the following models: In the earliest one by Schmid-Schonbein , leukocyte was modeled as a viscoelastic solid, with a Maxwell element in parallel with an elastic element. However, researchers have also shown that the deformation of leukocyte into a pipette is a continuous flow process, with no approach to a static deformation limit. They suggested that leukocyte could be modeled as a Newtonian liquid drop with a pre-stressed cortical tension. To get accurate result with Maxwell fluid model, material properties must vary with the amount of cell deformation. On the other hand, shear-thinning model fails to predict deformation during rapid recoil region, resulting in predicting different apparent viscosities in micropipette aspiration.
It has also been suggested that the correct mechanical model for leukocyte can only be obtained when it is true to the morphology of the cell and its content by taking into account internal structure of the cell. The model includes the most important physical components of the cell, namely the membrane cortex, the cytoplasm and the nucleus. Studies have concluded that the nucleus and its deformation must be included in the analyses of leukocytes to obtain a reliable understanding of mechanical and rheological properties of the cell behavior. Based on their axisymmetric model, they were able to study mechanical behaviors in some special cases. However, considering leukocyte subpopulation, many situations cannot be treated under the assumption of axisymmetry. For example in the case of neutrophils, which is the main leukocytes subpopulation, the cell nucleus is segmented. In this case, a full 3-dimensional description of the cell and nucleus becomes necessary to obtain a faithful representation of the cell. Research is being done to obtain a proper model and a better understanding of rheological and mechanical properties of leukocyte.
BIOLOGICAL CELL RHEOLOGY
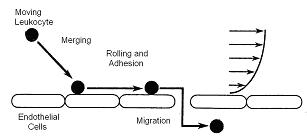
The objective of this research is to develop a comprehensive model of the processes that occur during rolling, merging, deformation, adhesion, and migration of a leukocyte in a shear flow. Such a model will then be used to obtain a better understanding of leukocyte behavior. To that end, a computational methodology that combines fluid dynamics and chemistry will be developed. Leukocytes (White blood cells) play an important role in the host defense system as they travel from the blood stream into the tissue in reacting to inflammatory stimuli such as cut and infection. Once initiated, chemoattractants (chemicals that attract leukocytes) are released and send signals to leukocytes. Leukocytes move towards the endothelium (cells at the interface of the blood and the vessel wall), away from the central blood stream, and roll along the wall of venules with a low velocity as compared to the surrounding erythrocytes (Red blood cells).
Leukocytes are then captured by the activated endothelium. Once they are captured, they may transiently adhere to the venular endothelium and begin to roll. Rolling occurs at or below the velocity of freely flowing cells such as erythrocytes in the same vessel and the same radial position. A firm adhesion is then initiated by activation of receptor-ligand between leukocytes and endothelial cells, which binds the membranes. The arrested leukocytes use these interactions to cross the endothelial lining of the blood vessel and migrate into the tissue.
MICRO-PIPETTE ASPIRATION
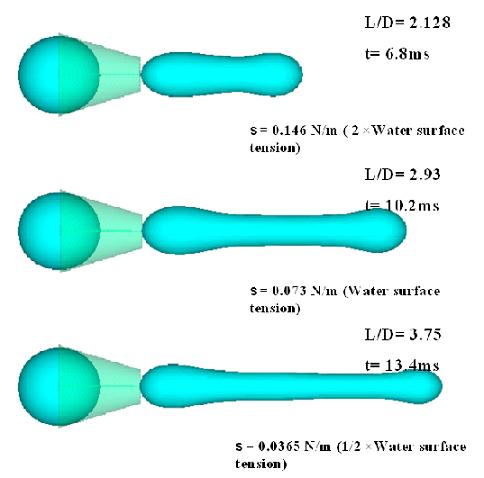
Continuous deformation and entry flow of single neutrophil into a micropipette is presented at various suction pressures to determine an apparent viscosity for the cell contents. For this purpose a computational methodology that reveals the dynamics of human neutrophils during micropipette aspiration has been considered. Micropipette aspiration is an important method in the research of the rheology of the resting neutrophil leukocyte. During this process the mechanical behavior of neutrophil is studied by aspirating the surface of the cell into a small glass tube while tracking the leading edge of its surface. Cell deformation and penetration into the pipette relates to its properties. Therefore, by measuring both the rate of cell deformation and the pressure, cell properties are determined. It has been shown that the neutrophil leukocytes exhibit a liquid-drop type behavior. When a neutrophil is aspirated by a pressure larger than a certain threshold pressure, it flows continuously into the pipette. In our model, the cell is approximated as simple slippery droplets of viscous homogenous Newtonian fluid with a constant surface tension.

For this passive cell, the rate at which it deforms under the action of a given pressure gradient is expected to be governed by the viscous dissipation in the cell interior (cytoplasm and nucleus) and membrane cortex. The behaviors of this model as a function of surface tension, aspiration pressure, pipette radius and viscosity have been investigated. Computation has been carried out by solving Navier-stokes equations in a three dimensional coordinate system. A negative pressure has been employed inside the pipette. Surface tension is modeled using the Continuum Surface Force (CSF). Deformations of the interfaces are tracked using volume-of –fluid (VOF) based model. Dynamics of the droplet deformation for different sizes of pipettes under various suction pressures are simulated. In the aspiration process, initial condition is determined by whether the aspiration pressure is sufficient to overcome the effects of surface tension. Therefore, first geometrical effects of surface tension have been studied while the other factors are constant. We have observed a pronounced flattening of the droplet against the outer walls of the pipette, which is due to low surface tension. These results are consistent with the ones obtained by Dury and Dembo1. However, at low capillary numbers, surface tension is sufficient to balance the suction pressure and droplet does not make contact with the exterior surface of the pipette. Also, comparing different sizes of pipettes shows that the best fit to our simulation is obtained when the pipette diameters are close to half of the cell diameter.
