OVERVIEW
AZIMUTHAL INSTABILITY OF A FERROFLUID LAYER
Instability of a ferrofluid layer with a finite thickness subject to a perpendicular magnetic field is subject to a perpendicular magnetic field is reported experimentally. The deformation of the fluid layer to individual spikes and the dynamics of these formed spikes are all studied and photographed. Two different methods, known as sudden field and increasing field are chosen to provide the necessary magnetic fields and proven to have significant impacts on the determination of the spike formation.
The surface dynamics of the fluid layer is divided with the definition of the critical and the supercritical magnetic field. The experiments show crucial evidences to the azimuthal instabilities to the fluid layer. Many parameters, such as diameters, heights, and generated number of the spikes are analyzed with different applied voltage.



INTRODUCTION TO FERROMAGNETIC FLUIDS
WHAT ARE FERROMAGNETIC FLUIDS?
Ferromagnetic fluids (ferrofluids) are colloidal fluids composed of small (3 to 15 nm) solid, magnetic, and single-domain particles (usually coated with a dispersant molecular layer), suspended in a liquid carrier. Due to their magnetic characteristics, ferrofluids have been successfully utilized in variety of field, such as in the energy generation devices to convert heat to work, in the sealing of feedthroughs and reciprocating shafts in the chemical engineering and in some commercial applications such as damping, heat transfer and bearings. More recently, ferrofluids have been used for remote positioning of small devices using the magnetic fields.


STUDIES OF FERROFLUIDS
The studies of the ferrofluids themselves are involved with rich understanding in physics and have revealed many interesting phenomena, unique to these fluids. The previous studies on the instability of the ferrofluids can be categorized into i) finite liquid layers and ii) large liquid drops. They show individual significance. However, no connection between these two categories has been performed to date to our knowledge. The present work is a link between these two groups of studies. Here, we study the instability of a finite ferrofluid layers resulting in the formation of fluid spikes and, further, the instability of individual spikes and their consequent breakup.
STUDY OF FINITE LIQUID LAYERS
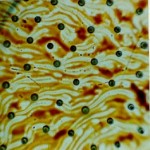
In studying ferrofluids, it is observed that liquid spikes are formed on the fluid surface upon application of a magnetic field. As a perpendicular magnetic field is applied to a ferrofluid layer, the surface disturbances of the ferrofluid are excited and the fluid surface becomes wavy. There is no need to apply actual vibrations. For a very thin layer applied with a magnetic field, the ferrofluid layer breaks into spikes and form a labyrinthine pattern. The geometric characteristics of these spikes depend on the intensity of the magnetic field.
Akhipenko et al. (1978) and Ceberes and Maiorov (1980) show the formation of comb type instability in a thin ferrofluid layer as the magnetic intensity increases. The ferrofluid layer attains a new equilibrium configuration depending on the intensity of the magnetic field. For a ferrofluid layer with an infinite thickness, Cowley and Rosensweig (1967) show that a critical magnetic field can be devised and is related to the ferrofluid properties and magnetization. The extension of the infinite ferrofluid layer to a finite layer bounded by a solid base is also studied.
EXPERIMENTAL APPARATUS AND PROCEDURE
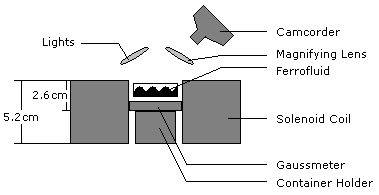
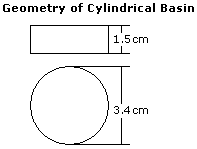
The magnetic field is generated using a solenoid coil. The container carrying ferrofluid is positioned at the center of the solenoid coil (2.6 cm from the top of the solenoid), such that a normal magnetic field H would be imposed on the ferrofluid. the solenoid coil is connected to a power supply. A Gaussmeter (F.W. BELL 4048) is located inside the solenoid coil to measure the intensity of the magnetic field exerted on the fluid. A commercially available oil-based ferrofluid (Ferrofluidics – EMG900G) is used for all the experiments. A cylindrical plastic container with a diameter of 3.4 cm and a height of 1.5 cm is the basin for the ferrofluid. The fluid is exposed to the ambient air. Both the air and the plastic container have very low susceptibility , and therefore each can be assumed to be zero.
The dynamics of the deformation of the ferrofluid surface is recorded using a conventional video camera. The intensity of the magnetic field is varied by changing the input power to the solenoid. Special attention is given to the instabilities in the azimuthal direction. in addition, the influence of the thickness of the fluid layer on its instability is investigated by using two different volumes of the fluid in the container: 1 ml and 2 ml.
Two different approaches are taken for the application of magnetic field:
1. Sudden Field: In this case the power supply in preset to a certain value to provide an expected magnetic field intensity to the container is located in test section, and the power supply is switched on. The magnetic force, the surface tension force and the gravitational force simultaneously act on the fluid and result in a sudden formation of a new equilibrium liquid topology. Enough time is allowed between each experiment that the surface deformation of the previous test does not influence the next test.
2. Increasing Field: In this case, initially a small field intensity is preset on the power supply (before it is switched on). Once the power supply is switched on, the power is slowly increased until the desired field intensity is reached. The results are affected by the preset value. Preset powers from 10 volts to 50 volts have been used. Very different types of spike formation is observed for each case as it will be discussed in the Experimental Results section.
EXPERIMENTAL RESULTS
Initially, when the power supply is turned off. the power level is preset to a certain value. Once the power is switched on, the ferrofluid layer is exposed to a uniform and upward magnetic field. The following figures show different surface topologies with increasing field intensity.

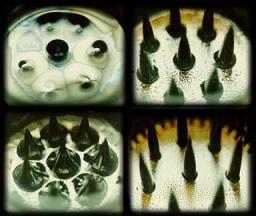
a)Lower Field: unperturbed surface

b)Critical Field: first peak generated

c)Transition: more peaks
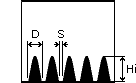
d)Supercritical Field: dispersed spikes(Hi: height, D: diameter, S: spacing)
At relatively low initial intensities, H, no surface deformation is observed. As the intensity is slowly increased, liquid surface becomes deformed. The intensity at which the first surface spike is observed is referred to as the critical field, Hcr. Figures (a) and (b) show the surface shapes for intensities below and above Hcr. As H is further increased, the number of spikes on the liquid surface increases, as represented in figure (c). In addition, the heights of these spikes increase with increasing field intensity. Eventually, the magnetic force breaks the surface of the fluid layer and separates the spikes from one another as shown in figure (d).
The magnetic field at which the fluid layer is fully separated into individual spikes is referred to as the supercritical field, Hsu. The critical field intensity, Hcr, at which the liquid layer becomes unstable and supercritical field intensity, Hsu, at which liquid layer breaks up into individual spikes depend on several parameters, including fluid properties (density r, viscosity m, surface tension s, and permeability of ferrolfuid c), volume of the fluid inside the container, and size and shape of the container.
CONCLUSION
The experimental study in a cylindrical ferrofluid layer with a finite thickness shows clear evidences of the azimuthal instability. The separation of the fluid layer to individual spikes is observed. These formed spikes continue to branch from their bottom and eventually are torn apart if the applied voltage is high enough. Two different methods are chosen in the application of the perpendicular magnetic field. A sudden field is useful in prediction of spike number whereas an increasing field may help in engineering design when a certain number of spikes is required. Different from a single droplet, some azimuthal surface ripples are captured close to the bottom of these generated spikes as the applied voltage is not high . However they are no observed at high voltage. On the contrary, the torus shape of the surround fluids exhibit the instability at high voltage. The parametric studies clarify the dynamics of this study. The adhesion effect is evaluated with comparison of two ferrofluid layer thickness.
